Educational Material
1.5 Advanced GNSS
While trilateration from pseudoranges can be used to calculate a user's position as discussed in Section 1.2, this method on its own is typically only able to provide a positioning accuracy on the order of several of meters (see Section 3.4). This section describes various advanced GNSS techniques that can be employed to achieve a higher positioning accuracy, and the signals that make them possible.
Signals
In order to understand the advanced GNSS positioning techniques, it is helpful to know more about the signals used in these methods. The following discussion focuses on the GPS constellation, but similar signals exist across all GNSS constellations.
L1, L2, L5 frequencies
The Global Positioning System (GPS) currently operates on three carrier frequencies known as L1, L2, and L5, as shown in Table 1.6. They are located on the L-band in the radar section of the electromagnetic spectrum and were chosen due to their ability to penetrate most atmospheric obstructions such as clouds, fog, or rain. In addition, ionospheric delay is much smaller for the frequency range of 1 GHz to 10 GHz, and frequencies below 2 GHz can be received without need for a beam antenna. Note that the L5 band is a recent development that is currently available on only a handful of satellites in the GPS constellation.
| NAME | FREQUENCY | APPLICATION |
|---|---|---|
| L1 | 1575.42 MHz | Civilian navigation |
| L2 | 1227.60 MHz | Military, but some civilian use |
| L5 | 1176.45 MHz | Precision guidance |
Carrier, Code (C/A and P(Y)), Navigation
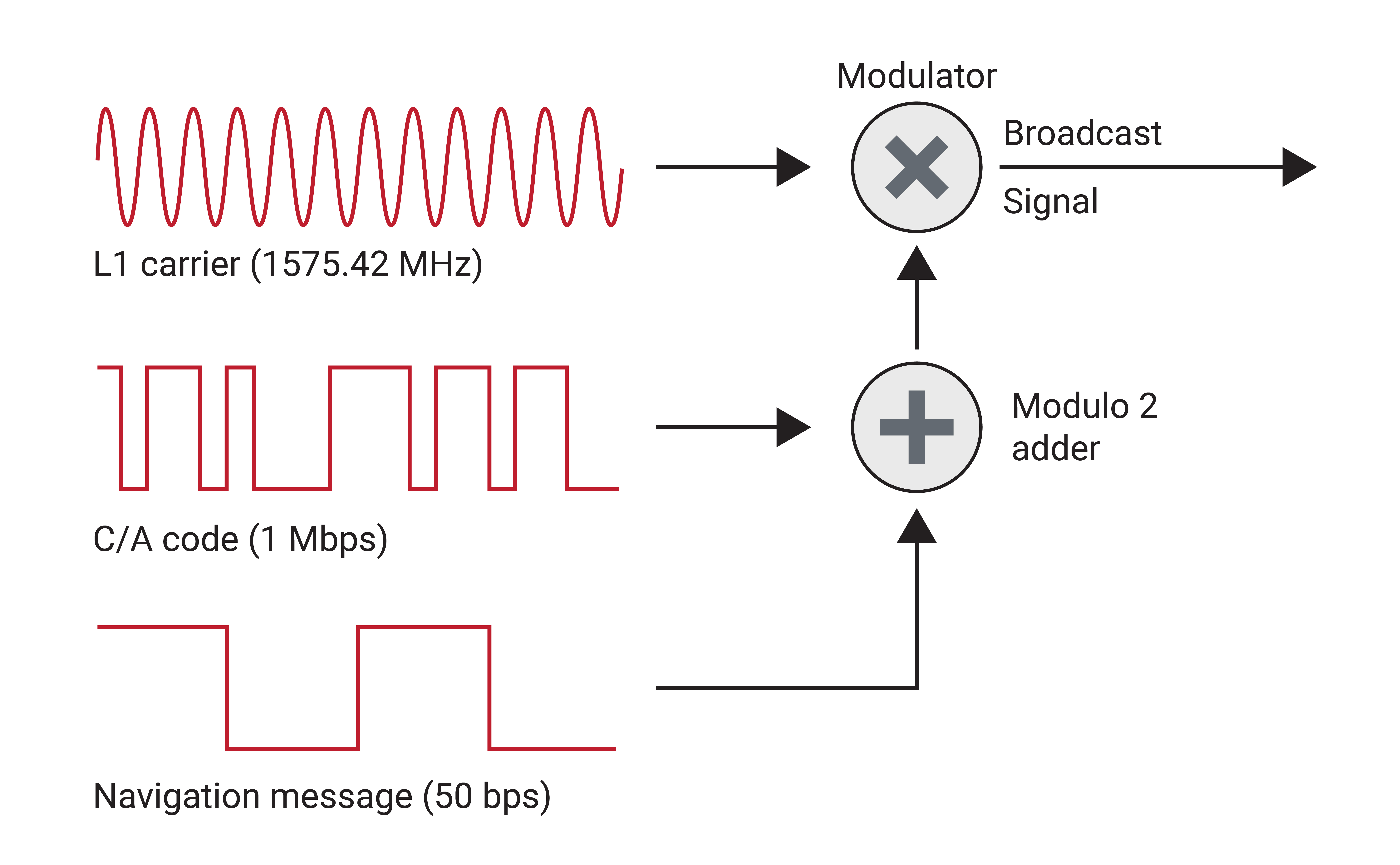
The GPS signal from each satellite is composed of three components called the carrier, the pseudo-random noise (PRN) code, and the navigation message. The PRN code signal gives each satellite a unique identifier which allows all satellites on the band to transmit on the same frequency without jamming. Coarse/acquisition (C/A) code is generated at 1.023 Mbps on the L1 band, while Precise code (P-code) is generated at 10.23 Mbps on L1 and L2. P-code is encrypted with W-code to become P(Y)-code, which acts as an anti-spoofing measure and is often used in military applications.
In an attempt to increase the security of military GPS systems, a code known as M-code has also been developed for the L1 and L2 bands. M-code provides additional protection against jamming due to its ability to be transmitted at a higher power. It is expected to eventually replace P(Y)-code, although uptake into the market has been slow.
The navigation message is a binary-coded representation of the GPS time, satellite health, ephemeris, and almanac data which the receiver uses to determine its position. Due to its slow speed of 50 bytes per second, the full message, broken into 25 frames, takes about 12.5 min to receive. Every frame, which each takes 30 s to transmit, includes the full GPS time and individual satellite health and ephemeris, allowing for a receiver to achieve a position solution before receiving the entire navigation message.
The code and navigation message are modulated onto a sinusoidal carrier signal as shown in Figure 1.12. The high frequency of the carrier signal allows transmission over the necessary distances and through adverse weather conditions on the way from the satellite to the receiver. The receiver then demodulates this signal to extract the original information.
Differential GPS (DGPS)
In order to overcome some inherent limitations of a single GPS receiver, multiple GPS receivers may be used in a technique known as Differential GPS, or DGPS.
Local-Area Augmentation System
DGPS requires some form of radio link between the receivers, and that one receiver have a well-known GPS location to serve as the base station. The signal transmitted from a single satellite to both the base station and rover receiver experiences the same satellite clock errors, orbit errors, and atmospheric propagation errors if the distance between them is below roughly 20 km. The base station can then determine an estimate of how much error is present compared to its already known location and transmit a pseudorange correction to a local receiver. Local-area DGPS systems can achieve positioning accuracy down to the one-meter level.
Satellite Based Augmentation System (SBAS)
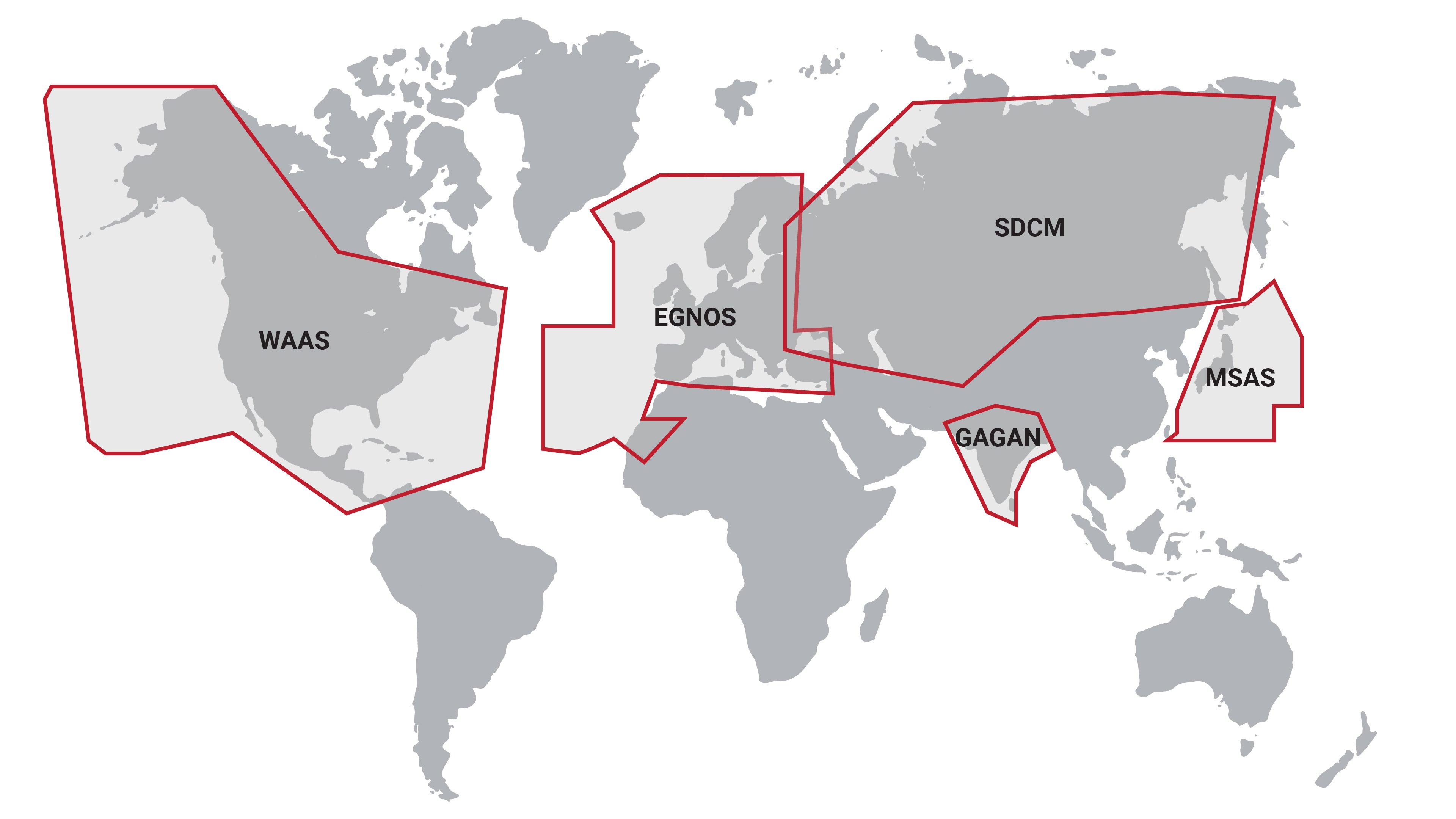
SBAS is a DGPS system where errors present at location-established reference stations are transmitted to a central location to compute differential corrections. These corrections are then broadcast over a region by geostationary satellites on the same L1 frequency as GPS, which receivers can track and use to obtain a positional accuracy of one to two meters. The map in Figure 1.13 illustrates the locations of SBAS systems in use, covering most of the Northern hemisphere. More information on each of these SBAS systems can be found in Table 1.7.
| REGION | NAME | ACRONYM | SATELLITES |
|---|---|---|---|
| North America | Wide-Area Augmentation System | WAAS | 2 |
| Europe | European Geostationary Navigation Overlay Service | EGNOS | 3 |
| Russia | System for Differential Corrections and Monitoring | SDCM | 4 |
| India | GPS-Aided GEO Augmented Navigation System | GAGAN | 3 |
| Japan | Multi-functional Satellite Augmentation System | MSAS | 2 |
Real-Time Kinematic (RTK) & Post-Processed Kinematic (PPK) Positioning
To achieve more precise location results, a multiple-receiver system called real-time kinematic (RTK) positioning was developed. Like differential GPS, RTK compares measurements between a base receiver and a rover receiver, but RTK relies on the carrier phase observables rather than the pseudoranges. Post-processed kinematic (PPK) positioning utilizes the exact same techniques and algorithms, but is computed offline on a PC, negating the need for computations to run in real time on the receiver or for a reliable real-time radio link for corrections.
Double-Differencing
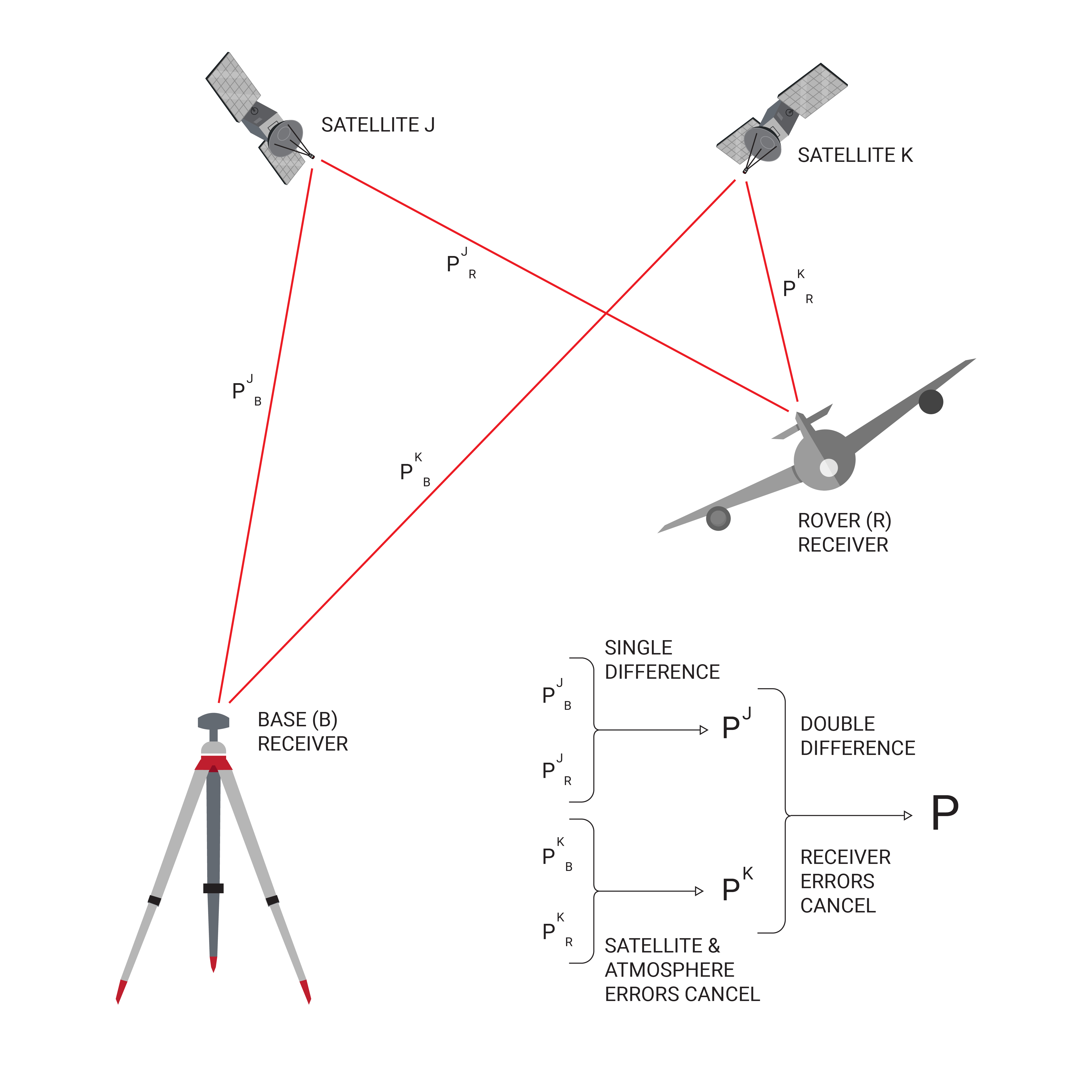
Carrier phase measurements are incredibly precise measures of the partial wave tracked between a satellite and a receiver. The difficulty is that the integer number of full wavelengths between the satellite and receiver is impossible to determine in a standalone GNSS configuration, a problem known as the integer ambiguity. Using double-differencing algorithms between two receivers, a related form of the integer ambiguity problem can be solved, yielding relative position accuracy to within two centimeters.
Double-differencing requires two receivers and two satellites. By differencing the carrier phase data between two satellites on a single receiver, most receiver errors (eg. receiver clock bias, including delays due to cable length) can be eliminated. Meanwhile, differencing the measurements from a single satellite between two different receivers eliminates the satellite-related errors (eg. orbit errors, atmospheric delays). Differencing these two differences---double-differencing---yields a result where most error sources have been eliminated. This process is summarized graphically in Figure 1.14.
Single vs. Dual Frequency
An important consideration for RTK or PPK systems is whether the receivers are tracking a single frequency (L1) or dual frequencies (L1/L2). When tracking only a single frequency, the integer ambiguity problem yields a large number of feasible solutions, making it difficult for a reliable RTK fix to be achieved and maintained. Utilizing an INS in combination with GNSS allows for much more robust tracking of the correct RTK fix in a single-frequency system, though initial acquisition can still take 10s of seconds to minutes. When two or more frequencies (with different wavelengths) are utilized, the intersection of feasible solutions to the integer ambiguities on each frequency is often a single point, leading to a near-instantaneous, reliable RTK fix.
Precise Point Positioning (PPP)
Like SBAS providing a base-station free differential correction, many private companies have developed satellite-based corrections services that can achieve real-time, centimeter-level accuracy without the added infrastructure of an RTK system. Precise point positioning (PPP) combines precise clocks, orbit locations, ephemeris, and atmospheric models with proprietary software algorithms to increase the ability of a receiver to determine its location. This information is transmitted to a receiver either from a geostationary satellite or over the internet, and requires a subscription and additional software specific to the company used. These L-band corrections are not transmitted on the same exact frequency as any GNSS signal, but are nearby in the frequency spectrum, so GNSS antennas can be designed to track both simultaneously. Using this additional data, accuracy down to 3 cm (<10 cm typical) is achievable globally without need for a base station or radio link. However, it is important to note is that PPP systems may take 20-40 minutes to converge on such a high-accuracy solution. Notable L-band correction services utilizing PPP systems include TerraStar, OmniStar, StarFire, and Veripos.
